Teorema de Pappus

O Teorema de Pappus é um dos teoremas fundamentais da geometria projectiva. Num certo sentido é o exemplo mais simples de um teorema de incidência. Neste exemplo vamos construir, passo a passo, uma instância dinâmica do teorema.

Criando o seu Primeiro Ponto

Quando inicia o Cinderella, a primeira janela que se abre corresponde à geometria euclideana. Esta janela inclui uma barra de ferramentas que é fundamental para operar com as funções disponíveis no programa. Em baixo dessa barra encontra-se a superfície de construção, onde irá efectuar as operações que quizer construindo e movendo elementos geométricos.

Note que um dos botões da barra de ferramentas está escurecido. Isto indica o modo em que o Cinderella se encontra.

Todas as acções do rato na superfície de construção se referem ao modo seleccionado. O modo activo agora é o "Criar ponto". Desloque o ponteiro para a superfície de construção e prima o botão esquerdo do rato. Um novo ponto é criado acompanhado por uma letra maiúscula.

Fig. 1: O seu primeiro ponto

Antes de criar mais pontos continue a ler. Se mantiver o botão esquerdo do rato premido enquanto adiciona um ponto, ainda o pode deslocar. O ponto será caracterizado pela situação geométrica da corrente posição do indicador do rato (para já não há muita geometria na sua superfície, mas isto vai mudar em breve). Desloque o indicador para a superfície de construção, prima o botão esquerdo do rato e, mantendo-o premido, mova o rato. Notará que o novo ponto se mantém agarrado à ponta do indicador. As coordenadas do novo ponto em cada posição são visíveis. Quando se aproxima de um ponto já existente (tente isto) o novo ponto salta para cima do outro. Só depois de largar o botão do rato o novo ponto é acrescentado à figura. Se largar o botão deixando o novo ponto cair sobe um outro, nenhum novo ponto é criado. Entretenha-se com estas funções e acrescente alguns pontos mais.

Fig. 2: Muitos pontos

Anular uma Operação

O seu ecrã pode estar atulhado. Há uma operação que inverte as acções que tiver realizado. Premindo o botão para anular o último ponto que tiver introduzido desaparecerá. Clique o botão anular até que somente dois pontos restem na superfície de construção. Pode usar este botão sempre que cometer um erro. Pode anular tantas operações consecutivas quantas quizer.

Movendo um Ponto

Queremos continuar a nossa construção do Teorema de Pappus. Coloque os dois pontos remanescentes A e B aproximadamente na posição ilustrada na Figura 3.

Fig. 3: Obtenha esta situação

Provavelmente os seus pontos não estarão nas posições indicadas. Para isso, seleccione o modo "mover" premindo o botão na barra de ferramentas. Agora a acção do rato já não consiste em acrescentar pontos; em vez disso pode pegar nos pontos e movê-los à vontade. Coloque o indicador do rato sobre um ponto que deseja deslocar. Prima o botão esquerdo do rato. Mantenha-o premido e arraste o rato. O ponto segue o movimento do indicador do rato. Também notará que, neste modo, o ponto não cai sobre outros pontos. Quando parar de premir o botão do rato o ponto é colocado de novo. Em geral, este modo permite mover todos os elementos livres de uma construção. O resto da construção mover-se-á em conformidade.

Juntando uma Recta

Vamos agora acrescentar uma linha recta de A para B. Mude para o modo "Criar recta" premindo o botão . Neste modo pode acrescentar uma recta por dois pontos usando uma sequência premir/arrastar/largar do rato. Coloque o indicador do rato sobre o ponto A. Prima o botão esquerdo do rato. Mantenha-o premido enquanto arrasta o indicador na direcção de B. Largue o botão.

Fig. 4: Criar uma recta

Esta acção deve ter criado a recta pretendida. Pode ter reparado em várias coisas. Quando deslocou o indicador sobre A este ponto ficou realçado. Isto significa que este ponto foi escolhido par primeiro ponto da recta. Enquanto desloca o rato está sempre presente outro ponto, na posição do indicador. Quando largar o botão do rato este ponto será criado. Quando se aproxima de outro ponto este fica realçado e o segundo ponto cai sobre ele. Nós usámos esta segunda acção para fazer a recta conter B.

Se não deu por estes fenómenos, ou se se enganou em algum passo, anule as operações efectuadas e tente de novo. A sua construção deve ser semelhante à Figura 4 antes de prosseguir.

Juntando mais Rectas

Agora está pronto para juntar mais algumas rectas e obter algo como a Figura 5. Pode fazê-lo com três operações do rato. Primeiro, coloque o indicador sobre B prima o botão esquerdo do rato, mantenha-o premido e arraste o rato até criar o ponto C. Execute outra destas operações entre C e D, e finalmente, entre D e E.

Fig. 5: Mais rectas

Note que realizou tudo isto sem sair do modo "Criar recta". Realizou algum trabalho desnecessário quando criou os pontos A e B no modo "Criar ponto". Poderia obter o mesmo resultado usando o modo "Criar recta", porque não só o segundo ponto pode ser assim criado, mas também o primeiro. As rectas já criadas receberam automaticamente as etiquetas formadas pelas letras minúsculas a até d.

Criando Pontos de Intersecção

Mantenha-se no modo "Criar recta". Agora queremos acrescentar a recta que contém E e a intersecção das rectas a e c. Coloque o indicador do rato sobre E. Prima o botão esquerdo do rato e mantenha-o pressionado enquanto se desloca para a intersecção de a e c. Largue o botão.

Fig. 6: Juntando uma intersecção

Quando se aproximou da intersecção das rectas estas ficaram realçadas e o ponto caiu automaticamente sobre a intersecção. Quando largou o botão do rato o ponto criado foi definido como o ponto de intersecção das rectas. Quando mover os pontos de A a E a nova recta mover-se-á em conformidade.

O novo ponto F está desenhado com uma cor mais escura. Isto significa que não é possível mover F livremente no modo "mover". F é um ponto "dependente". Os outros pontos numa construção são "livres".

Há duas observações importantes: Com o mesmo procedimento podia ter-se acrescentado um ponto "semi-livre", confinado a mover-se numa recta, só teria de largar o botão do rato quando estivesse sobre uma das rectas. Todas estas operações de criação de intersecções, pontos livres ou semi-livres, funcionam no modo "Criar ponto". Muitos outros modos, interactivos, também dispoem destas facilidades. Consulte as referências deste manual para mais informações.

Acabando o Desenho

Agora terá facilidade em terminar a construção acrescentando quatro rectas mais. A configuração final é mostrada na Figura 7. Primeiro acrescente uma recta por A e pela intersecção de b e d. Depois desenhe duas rectas, uma por A e D e outra por B e E. Finalmente junte uma recta por C e pela intersecção de e e f.

Fig. 7: Teorema de Pappus

Terá até agora construído oito pontos e nove rectas. Se observar a sua construção reparará que, se tudo foi construído corretamente, as rectas g, h e k têm um ponto comum. Que isto acontece sempre em tal construção é o conteúdo do Teorema de Pappus. Mude para o modo "mover" clicando na barra de ferramentas, e mova os pontos livres da sua construção de forma a convencer-se da veracidade deste teorema. Este resultado já era conhecido dos geómetras gregos. Mais tarde veio a revelar-se de importância fundamental em Geometria Projectiva.

Seleccionando e Alterando o Aspecto

Talvez não lhe agrade a aparência da sua construção. As rectas podem ser demasido finas e talvez queira enfatizar a conclusão do teorema. Seleccione o item do menu "Propriedades/Editor de Aspecto". A seguinte janela surgirá:

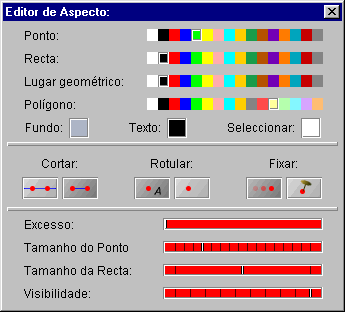Fig. 8: O Editor de Aspecto

Alterações no Editor de Aspecto têm efeito imediato nos elementos seleccionados. Primeiro prima o botão "Seleccionar todas as rectas" . Se agora mover a escala móvel "Tamanho de recta" no Editor de Aspecto até à segunda marca, todas as rectas se tornarão mais grossas. Depois disto mude para o modo "Seleccionar" . Agora, quando clicar sobre um elemento, este será seleccionado. Se mantiver premida a tecla "shift" quando clicar, o estado do elemento mudará (seleccionado/não seleccionado).

Clique sobre a recta k, depois, mantendo premida tecla "shift", clique sobre as rectas h e g. As rectas g, h e k devem estar realçadas. Clique na caixa vermelha na segunda linha da paleta de cores do Editor de Aspecto. A cor das três rectas muda de azul para vermelho. Também pode alterar a espessura das rectas fazendo deslizar o marcador da escala móvel para a terceira marca. Por fim desseleccione tudo premindo o botão .

Fig. 9: Aspecto alterado

Juntando um Ponto Final e Provando um Teorema

Antes de continuar abra a Janela de Informação do Cinderella, escolhendo o item "Vistas/Janela de Informação" do menu. Uma janela abre-se. Cinderella usa esta janela para relatar factos não triviais de uma configuração.

Criaremos agora um último ponto, na intersecção das três rectas vermelhas. O modo "Criar ponto" não é o apropriado nesta situação porque Cinderella recusa-se a criar um ponto na intersecção de três rectas, dada a ambiguidade da situação. Contudo, pode acrescentar um ponto ponto se mudar para o modo "Intersectar" . Neste modo deve seleccionar duas rectas. O respectivo ponto de intersecção será acrescentado à configuração. Clique sobre duas das rectas, g e h por exemplo. O novo ponto será criado.

Fig. 10: O ponto de intersecção

Note que o novo ponto, K, está sempre sobre a recta k, devido ao teorema de Pappus. A consola relata este facto notável automaticamente.

Fig. 11: Um teorema demonstrado

Pode perguntar-se come é que esta capacidade de prova funciona. Cinderella não usa métodos simbólicos para criar uma prova formal, mas sim uma técnica chamada "Verificação Aleatória de Teoremas". Primeiro é gerada a conjectura "Parece que a recta k contém sempre o ponto K". Depois a configuração é movida em muitas direcções e, para cada uma delas, a conjectura é testada. Pode parecer ridículo, mas gerando aleatoriamente um número suficiente de exemplos em que a conjectura se verifica é, pelo menos, tão convincente como uma prova simbólica gerada por computador. Cinderella usa este método sistematicamente para manter os seus dados internos consistentes.

Movendo Pontos para o Infinito

Exploremos a simetria do teorema de Pappus. Para melhorar a aparência da figura podemos apagar todos os nomes das rectas e adelgaçá-las. Comece por seleccionar todas as rectas premindo . Desligue o etiquetar premindo o correspondente botão no Editor de Aspecto. Mude a espessura das rectas para "fino" (use a escala móvel). Agora escolha a opção "Vistas/Esférica". O que vai ver agora não parece muito instrutivo.

Fig. 12: Uma vista esférica

Trata-se de uma projecção central de um plano sobre a superfície de uma esfera. O centro de projecção é o centro da esfera (ver Fig. 13). Cada ponto é transformado num par de pontos antípodas, e cada recta é transformada num meridiano da superfície da esfera.

Fig. 13: Projecção do plano sobre a esfera

Na vista esférica há uma pequena escala móvel vermelha para controlar a distância da esfera ao plano original. Mover esta escala corresponde a efectuar um zoom na esfera. Mova o cursor para a direita. A situação na esfera deve ter-se tornado mais clara. Se ajustou o cursor correctamente deve ter obtido algo semelhante à Fig. 14. Reconhecerá agora com facilidade a sua construção na superfície esférica.

Fig. 14: O Teorema de Pappus numa esfera

A figura carece de explicação: Para cada ponto do plano considere a recta definida por esse ponto e pelo centro da esfera. A intersecção desta recta com a superfície esférica dá-nos o par de pontos antípodas. Para cada recta considere o plano que ela e o centro da esfera definem. A intersecção deste plano com a superfície da esfera é o meridiano que representa a recta na vista esférica.

Na esfera há pontos que não correspondem a nenhum ponto do plano euclideano. Se a esfera for tangente ao plano no seu "pólo sul" então o equador corresponde aos pontos no infinito no plano euclideano usual. O Cinderella permite efectuar manipulações em qualquer vista que esteja activa. Pode, portanto, mover pontos também na superfície esférica. As alterações serão imediatas também na vista euclideana. Em particular, pode deslocar um ponto para infinito na vista esférica.

É isso que faremos agora para exibir uma interessante simetria tripla da nossa configuração. Na vista esférica mova o ponto A para a posição correspondente às 11 horas do mostrador de um relógio. Este ponto fica agora "no infinito". Repare que as rectas euclideanas por A são agora paralelas: "Rectas paralelas encontram-se no infinito". De forma semelhante, mova E para a posição das 7 horas e C para as 3 horas. A sua vista esférica deve agora assemelhar-se à Fig. 15. Na vista euclideana encontrará três feixes de rectas paralelas. Observará uma espécie de instância euclideana do teorema de Pappus. Pode procurar o enunciado correspondente, àcerca de rectas paralelas e incidências.

Fig. 15: Uma simetria tripla

Pode acontecer que uma vista euclideana seja demasiado grande ou demasiado pequena. Pode usar os utensílios de zoom para as corrigir. Há um "aproximar" e um "afastar" em baixo da vista euclideana. Com uma sequência premir/arrastar/largar do rato pode marcar uma região sobre a qual incidir o zoom.