As vistas

A opção "Vistas" na barra de ferramentas oferece a possibilidade de abrir janelas com diferentes vistas de uma construção. Cada vista é uma espécie de "projecção" da configuração abstracta numa parte visível do ecrã. Normalmente pode efectuar construções e manipulações em qualquer vista. As alterações são imediatamente transmitidas às outras vistas. Em particular pode ter várias vistas do mesmo tipo (por exemplo várias vistas euclidianas, com escalas diferentes).

As vistas estão também relacionadas com as diferentes geometrias. Qual vista é apropriada para uma dada geometria está explicado na secção "Vistas e geometrias".

Vista euclidiana

A vista euclidiana é a superfície de construção habitual. Quando Cinderella arranca mostra uma janela com uma vista euclidiana. É a janela natural para fazer Geometria Euclidiana.

Teorema de Pascal numa vista euclidiana

A vista euclidiana dispõe de botões específicos. Podem ser utilizados como zoom e para translações. Também há controles para o quadriculado e os pontos atractores.

Efectuar Translacção

Este modo permite transladar todo o sistema de coordenadas. Com este modo seleccionado pode mover a vista arrastando o rato com o botão esquerdo premido.

Aproximar

Neste modo pode aproximar-se do seu desenho. Há duas formas de o fazer:

Afastar

Neste modo pode afastar-se do seu desenho. Há duas formas de o fazer:

Ver todos os pontos

Ao premir este botão o zoom ajusta-se de forma a mostrar todos os pontos da construção.

Alternar quadriculado

Mostra/esconde um quadriculado na vista.

Alternar eixos

Mostra/esconde um sistema de eixos coordenados na vista.

Alternar atractores

Alterna o modo "atrair". Neste modo os pontos do quadriculado são magnéticos e atraem o ponteiro do rato. Este é o modo ideal para desenhos rigorosos. Se escolher este modo à partida o quadriculado e os eixos serão automaticamente visíveis. Podem ser individualmente escondidos.

Quadriculado mais fino

Dá um quadriculado mais denso.

Quadriculado mais grosso

Dá um quadriculado menos denso.

Usando "atractores" para desenhos rigorosos

Vista esférica

A vista esférica advém da projecção do plano sobre uma superfície esférica. O centro de projecção é o centro da esfera. O plano não contém este centro.

Projecção do plano sobre a esfera

Cada ponto é transformado num par de pontos antípodas, e cada recta é transformada num meridiano da superfície da esfera. A estrutura de incidência é preservada. Trabalhar com a vista esférica permite manipular elementos no infinito, que estão na fronteira da imagem da esfera.

O Teorema de Pappus numa esfera

A vista esférica é a forma natural de representar Geometria Elíptica. Medições de ângulos entre rectas correspondem a medições sobre a superfície esférica. Medições de distâncias correspondem às medições geodésicas usuais, tendo presente que pontos antípodas são identificados.

Rotação

Este modo permite rodar a vista esférica (após a projecção). Neste modo pode rodar a vista movendo o rato com o botão esquerdo premido.

Reset da esfera

Esta acção recoloca a esfera na sua posição original. Após o reset a fronteira visível da esfera corresponde de novo à recta no infinito.

A escala móvel

Esta escala permite controlar a distância da esfera ao plano euclidiano. Pode usá-la para obter a ampliação óptima do seu desenho.

Vista hiperbólica

A vista hiperbólica é o modo natural para a Geometria Hiperbólica. De facto, fazer Geometria Hiperbólica é a principal razão para abrir uma vista hiperbólica. A vista hiperbólica representa uma implementação do modelo de Poincaré para a Geometria Hiperbólica. Neste modelo a parte finita do plano hiperbólico é representada por um disco. cada recta é representada por um arco circular ortogonal à fronteira do disco. As medições de ângulos são conformes. Isto significa que pode obter as medições medindo os ângulos euclidianos definidos pelos arcos de circunferência. As medições de distâncias colocam os elementos na fronteira infinitamente distantes de qualquer ponto no disco. Se se deslocar em passos hiperbolicamente unitários em direcção à fronteira, nunca a atingirá. No disco os passos parecem diminuir (na medição euclidiana).

Circunferências hiperbólicas de igual raio Alturas hiperbólicas são concorrentes

Vistas euclidiana e esférica duais

Dualidade é um conceito importante em Geometria Projectiva. Devido à completa simetria entre pontos e rectas é possível transformar qualquer enunciado sobre incidência de pontos e rectas no enunciado "dual", onde pontos e rectas trocaram de lugares.

Cinderella oferece duas vistas duais para visualizar a dualidade. A dualidade implementada no Cinderella é a dualidade relativa à matriz identidade. Em termos algébricos, usámos as coordenadas homogéneas de um ponto e interpretámo-las como as de uma recta, e vice-versa. Geometricamente isto é mais facilmente interpretado na vista esférica. Sempre que tiver um ponto, considere-o como sendo o pólo norte, o equador será a sua recta dual. Sempre que tiver uma recta considere-a como sendo o equador, o pólo norte será o seu ponto dual. A figura abaixo mostra uma configuração numa vista esférica e a sua dual.

Uma configuração... ...e a sua dual

Pode seleccionar elementos duais mas não os pode mover. Se os quiser deslocar tem de os controlar na vista primitiva.

Texto de construção

O texto de construção é uma descrição dos passos de construção. Cada elemento da construção geométrica é representado por uma linha na janela do texto de construção.

Uma imagem do teorema de Tales

Cada linha mostra um ícone que se assemelha ao elemento a que se refere. O ícone é mostrado com o mesmo tamanho, a mesma cor e a mesma forma do elemento respectivo. Isto facilita a identificação dos diversos elementos.

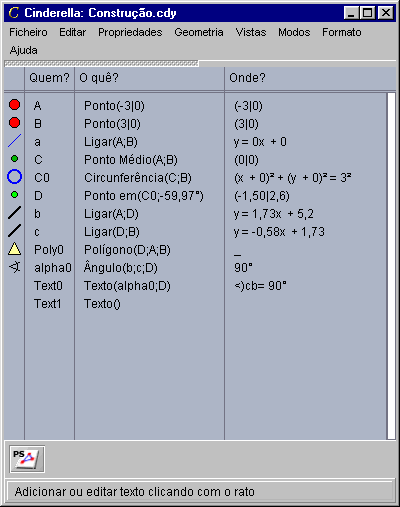Os passos da construção do teorema de Tales

O texto de construção consiste em quatro colunas. A primeira mostra os ícones. A segunda mostra as etiquetas dos elementos geométricos. A terceira explica a definição de cada elemento. A quarta coluna dá o valor actual do elemento. Na maioria dos casos trata-se da localização relativamente aos eixos coordenados. Com o menu "Formato" pode alterar a forma de mostrar a localização ou os valores dos elementos.

Os textos que aparecem no "Texto de construção" são exactamente as três entradas que podem ser referenciadas pelo modo "Criar texto".

As quatro colunas são separadas por linhas verticais. Pode seleccionar estas linhas com o rato para controlar a largura de cada coluna.

Funções gerais

Em cada vista uma barra de ferramentas em baixo permite operações específicas a cada vista. As comuns às três vistas são descritas abaixo.

Gerar PostScript

Se premir este botão o conteúdo da vista será exportado para um ficheiro PostScript. Ser-lhe-á perguntado se quer a figura a cores, tons de cinzento ou preto e branco. O ficheiro gerado contém uma secção inicial onde poderá, mais tarde, ajustar o aspecto da impressão. Começa assim:


   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   % Drawing mode:                                 %
   % mode=0: color  /  mode=1: gray  /  mode=2: bw %
   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   /mode 0 def

Mudando o modo pode mais tarde optar por uma representação a cores. Também pode alterar a cor de fundo.

   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   % Background color  (default white)             %
   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   /background { 1 1 1} def

As outras definições no ficheiro PostScript são de fácil interpretação.

Escolher geometria

Com estes botões pode alterar a escolha da geometria. Todas as construções são relativas a esta geometria. Para uma discussão detalhada das geometrias consulte os capítulos "Geometrias" e "Bastidores".

---> O Editor de Aspecto

<--- Geometrias

<--> Índice