Decida sobre a consistência de cada um. Em caso de consistência atribua valores de verdade às proposições atómicas de forma a que as premissas sejam todas verdadeiras; caso contrário deduza formalmente uma contradição.
- Se o Óscar estudar passa a Lógica. Se não estudar também passa. Contudo o Óscar não passa a Lógica.
- Se o Óscar estudar ele passa a Lógica ou a Matemática. Contudo, o Óscar não estuda, mas passa a Lógica ou a Matemática.
- Se a Maria estudar e o Óscar não a distrair, a Maria passa a Lógica e a Matemática. O Óscar não distrai a Maria. Contudo, a Maria chumba a matemática.
- Se o Óscar estudar ele acaba o curso este semestre ou no próximo. Se acabar este semestre ele vai fazer um mestrado. Se acabar no próximo ele não vai fazer um mestrado. O Óscar estuda.
- Se a Maria estudar ela vai acabar o curso. Se ela acabar o curso vai fazer um mestrado e casar-se. Se for fazer um mestrado a Maria não terá filhos este ano, mas se se casar então terá filhos este ano. A Maria não estuda mas acaba o curso.
- A Maria acaba o curso a menos que se case. A Maria vai trabalhar se e só se se casar. Se ela for trabalhar então não pode ajudar a Ana nos trabalhos de casa. Se a Maria não ajudar a Ana nos trabalhos de casa, a Ana não acaba o curso. A Maria acaba o curso se e só se a Ana não acabar.
- Se o Óscar estudar para o exame então ele não vai às docas na sexta-feira. Se o Óscar não estudar para o exame então ele não acaba o curso. Se ele não acabar o curso então não arranja emprego. Se o Óscar não for às docas na sexta-feira ele não encontrará a Ana. Contudo o Óscar arranja emprego e encontra a Ana.
- Se o Óscar e a Virgínia têm a mesma idade então o Jorge e a Maria não têm a mesma idade. O Óscar e a Virgínia têm a mesma idade ou o Óscar é mais velho que a Virgínia. Se o Óscar é mais velho que a Virgínia então ele é mais velho que a Maria. Não é verdade que se o Jorge e a Maria tiverem a mesma idade então o Óscar é mais velho que a Maria.
- Se o Óscar e o Jorge acabarem os seus cursos, então um deles vai arranjar emprego. Se o Óscar arranjar emprego então o Jorge não. Se o Jorge acabar o curso então o Óscar não. Nenhum deles acabou o respectivo curso, mas um deles arranjou emprego.
- Se o Óscar acabar o curso então o Jorge e a Virgínia também. Se o Óscar não acabar o curso então o Jorge acaba o curso e arranja um emprego. Se o Jorge acabar o curso então, se aranjar emprego, a Virgínia também arranja emprego. Se a Virgínia acabar o curso então o Jorge arranja emprego. Se a Virgínia arranjar emprego então o Jorge não acaba o curso.
- Se
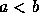 e
e 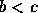 então
então
 . Se
. Se 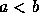 e
e 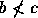 então
então
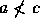 . Se
. Se 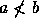 e
e 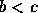 então
então
 . Contudo,
. Contudo,  sse
sse 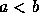 e
e 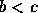 ou
ou 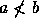 .
. - Se
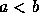 , então
, então 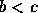 só se
só se  . Se
. Se 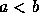 e
e
 , então
, então 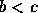 ou
ou 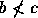 . Se
. Se 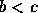 então
então 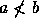 .
Contudo,
.
Contudo, 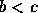 a não ser que
a não ser que 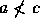 .
.
Nos exercícios seguintes considere uma frase do tipo "P é verdadeira" uma proposição atómica.
- Se a proposição condicional
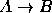 é falsa então
é falsa então
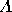 é verdadeira e
é verdadeira e 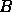 é falsa. A
proposição condicional
é falsa. A
proposição condicional 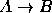 é falsa.
é falsa. - Uma condição necessária e suficiente para a proposição
condicional
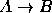 ser verdadeira é que ambas
ser verdadeira é que ambas
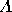 e
e 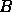 sejam verdadeiras. Uma condição
suficiente para
sejam verdadeiras. Uma condição
suficiente para 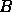 ser falsa é que
ser falsa é que 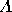 seja verdadeira. Uma condição necessária para a proposição
condicional
seja verdadeira. Uma condição necessária para a proposição
condicional 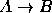 ser verdadeira é que
ser verdadeira é que
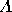 seja verdadeira. Contudo, a proposição condicional
seja verdadeira. Contudo, a proposição condicional
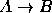 é falsa.
é falsa. - Se
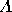 é falsa a proposição
condicional
é falsa a proposição
condicional 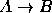 é da forma
é da forma 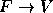 ou
ou 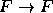 , conforme
, conforme 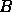 é verdadeira ou falsa, respectivamente. A proposição condicional
é verdadeira ou falsa, respectivamente. A proposição condicional
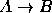 é da forma
é da forma 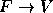 se
se 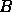 é verdadeira e
é verdadeira e 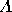 é falsa, mas nem
é falsa, mas nem
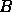 é verdadeira nem
é verdadeira nem 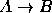 é da forma
é da forma
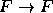 .
. - Se
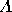 é verdadeira, a proposição
condicional
é verdadeira, a proposição
condicional 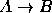 é da forma
é da forma 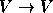 se
se 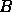 é verdadeira, e da forma
é verdadeira, e da forma
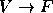 se
se 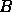 é falsa. Se
é falsa. Se 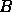 é falsa
é falsa 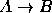 é falsa. Contudo,
é falsa. Contudo, 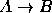 não é da forma
não é da forma 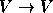 , e é
verdadeira.
, e é
verdadeira. - Se
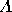 é falsa a proposição
condicional
é falsa a proposição
condicional 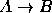 é verdadeira, e se
é verdadeira, e se
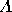 é verdadeira a proposição condicional
é verdadeira a proposição condicional 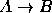 é verdadeira se
é verdadeira se 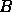 for verdadeira.
Uma condição suficiente para
for verdadeira.
Uma condição suficiente para 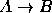 ser verdadeira é
que
ser verdadeira é
que 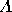 seja verdadeira e
seja verdadeira e 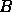 seja falsa. Contudo, a proposição condicional
seja falsa. Contudo, a proposição condicional
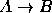 é falsa.
é falsa. - Se a função
 é contínua no intervalo
é contínua no intervalo
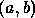 , então
, então  tem um máximo e um mínimo
em
tem um máximo e um mínimo
em 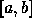 desde que
desde que  seja contínua em
seja contínua em  e
e 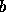 . A função
. A função  não tem um máximo em
não tem um máximo em
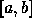 só se
só se  não for contínua em
não for contínua em
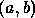 ;
;  não tem um mínimo em
não tem um mínimo em
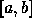 só se
só se  não for contínua em
não for contínua em
 . Se
. Se  tem um máximo em
tem um máximo em
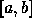 então
então  é contínua em
é contínua em 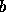 , mas se
, mas se  tem um mínimo em
tem um mínimo em
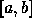 então
então  não é contínua em
não é contínua em
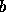 . Neste caso
. Neste caso  é contínua em
é contínua em
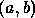 .
. - A função
 é contínua em
é contínua em 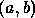 ,
,  é contínua em
é contínua em  e
e 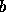 , e
, e  tem um máximo em
tem um máximo em
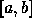 , mas não tem mínimo em
, mas não tem mínimo em 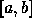 . Se
. Se
 é contínua em
é contínua em 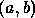 , então
, então
 tem um máximo e um mínimo em
tem um máximo e um mínimo em 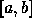 ou
ou  não é contínua
simultaneamente em
não é contínua
simultaneamente em  e
e 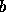 .
. - Se
 é contínua em
é contínua em 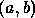 , então
, então  tem um máximo em
tem um máximo em
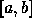 se
se  é contínua em
é contínua em  , e
, e  tem um mínimo em
tem um mínimo em 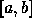 se
se  é contínua em
é contínua em 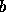 . Se
. Se  tem um máximo em
tem um máximo em 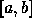 , então
, então  não é contínua em
não é contínua em
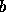 . Se
. Se  é contínua em
é contínua em 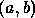 então
então  é contínua em
é contínua em  e
e 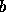 . Se
. Se  tem um máximo em
tem um máximo em
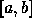 ou
ou  não tem um mínimo em
não tem um mínimo em
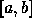 , então
, então  é contínua em
é contínua em 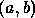 . Se
. Se  é contínua em
é contínua em  ou se
ou se  não tem um máximo em
não tem um máximo em
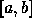 , então
, então  é contínua em
é contínua em 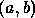 .
.
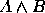 ,
, 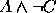
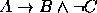 ,
, 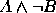
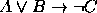 ,
, 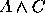
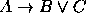 ,
, 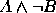
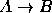 ,
, 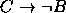 ,
,
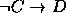 ,
, 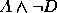
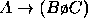 ,
, 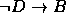 ,
,
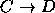 ,
, 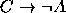 ,
, 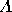
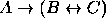 ,
, 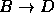 ,
,
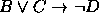 ,
, 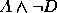
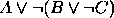 ,
, 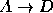 ,
,
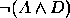 ,
, 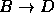 ,
, 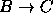
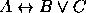 ,
, 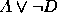 ,
,
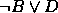 ,
, 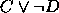 ,
, 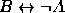
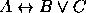 ,
, 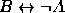 ,
,
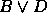 ,
, 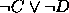
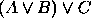 ,
, 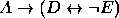 ,
,
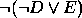 ,
, 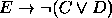 ,
, 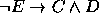 ,
,
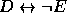
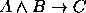 ,
, 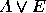 ,
,
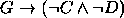 ,
, 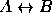 ,
, 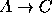 ,
,
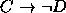 ,
, 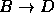 ,
, 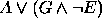
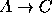 ,
, 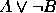 ,
,
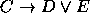 ,
, 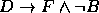 ,
, 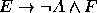 ,
,
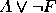 ,
, 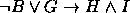 ,
, 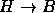
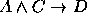 ,
, 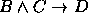 ,
,
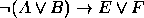 ,
, 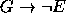 ,
, 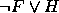 ,
,
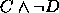 ,
, 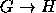
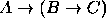 ,
, 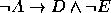 ,
,
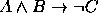 ,
, 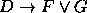 ,
, 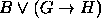 ,
,
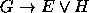 ,
, 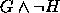
- i)
- Determine, em cada caso, se os testemunhos são consistentes.
- ii)
- Se os inocentes falam verdade e os culpados mentem, determine, se possível, quem é culpado e quem é inocente.
- Artur: O Belmiro ou o Cassius é culpado, mas eu estou
inocente.
Belmiro: Se a Desdémona é culpada então todos os outros somos inocentes.
Cassius: Se o Belmiro é culpado eu sou inocente.
Desdémona: O Artur ou o Belmiro é inocente.
- Artur: Se o Belmiro ou o Cassius é inocente então eu
també sou.
Belmiro: o Artur é culpado, e o Cassius ou a Desdémona também.
Cassius: Se o Belmiro é inocente então a Desdémona é culpada.
Desdémona: Se o Belmiro é culpado então o Cassius é inocente;
- Artur: Das duas, uma: ou o Belmiro é culpado e o Cassius
é inocente ou o Belmiro é inocente e o Cassius é culpado.
Belmiro: Se o Artur ou a Desdémona é inocente, então o Cassius também é.
Cassius: O Artur ou o Belmiro é culpado, mas eu sou inocente.
Desdémona: O Belmiro está inocente ou o Cassius é culpado se e s
- Artur: Ou eu sou inocente ou a Desdémona é culpada.
Belmiro: Se o Cassius é culpado então a Desdémona está inocente.
Cassius: Se eu sou inocente então o Belmiro é culpado.
Desdémona: Se o Artur está inocente então o Belmiro também.
- Artur: A Desdémona está inocente ou o Belmiro é culpado.
Belmiro: O Cassius é inocente ou a Desdémona é culpada.
Cassius: O Artur está inocente ou ou a Desdémona é culpada, e o o Artur é culpado.
Desdémona: o Artur está inocente se e só se ou o Belmiro ou o Cassius é inocente.
i) Determine se as seguintes afirmações são consistentes. ii) Em caso afirmativo as profissões de cada um pode ser determinadas de forma única?
-
- (a)
- V não é B nem C.
- (b)
- A não é P nem V.
- (c)
- B é V ou T.
- (d)
- C é V ou L.
-
- (a)
- P não é A nem B.
- (b)
- T não é A nem D.
- (c)
- V não é A ou C.
- (d)
- B é V ou L.
-
- (a)
- T não é A nem D.
- (b)
- V não é A nem B.
- (c)
- B é L ou P.
- (d)
- B é V ou L.
-
- (a)
- A não é L.
- (b)
- B não é P.
- (c)
- C não é T.
- (d)
- D não é V.
- (e)
- V não é A nem B.
- (f)
- L não é C nem D.
- (g)
- T não é A nem D.
-
- (a)
- L não é A nem D.
- (b)
- P não é B nem C.
- (c)
- T não é B nem C.
- (d)
- V não é C nem D.
- Encontramos três nativos--R, S, T--que dizem o seguinte:
- (a)
-
- R:
- Somos todos Ves.
- S:
- Exactamente um de nós é um Ve.
- T:
- Exactamente dois de nós são Ves.
- (b)
-
- R:
- Nenhum de nós é Ve.
- S:
- Exactamente um de nós é Ve.
- (c)
-
- R:
- S e T são do mesmo tipo.
- S:
- Eu e T somos Ves.
- T:
- S é Fa.
- (d)
-
- R:
- S e T são Fas.
- S:
- R é Ve.
- T:
- R é Ve.
- (e)
-
- R:
- S e T não são do mesmo tipo.
- S:
- R é um Ve.
- T:
- R é um Ve.
- De novo em FaVe encontrmos três nativos--U, V, W-- e
perguntamos-lhes: Quantos de vós sois Ves? A primeira
pessoa a responder, U, fá-lo na sua língua, que nós não entendemos.
Depois...
- (a)
-
- V:
- U disse "Exactamente um de nós é um Ve".
- W:
- Não acreditem em V, V é um Fa.
- (b)
-
- V:
- U disse "Exactamente um de nós é um Ve".
- W:
- V disse a verdade.
- (c)
-
- V:
- U disse "Todos somos Ves".
- W:
- Isso é mentira, V é um Fa.
- (d)
-
- V:
- U disse "Nenhum de nós é um Ve".
- W:
- Se V mentiu então U é um Ve.
- (e)
-
- V:
- U disse "V e W são Ves".
- W:
- V não disse a verdade.
- Uma mutação genética aconteceu em FaVe: nasceu uma criança, o
Sinão, que mente e diz a verdade alternadamente. Nunca s
- (a)
- Encontramos três crianças na ilha--X, Y e Z--e sabemos que uma
delas é o Sinão, outra é um Ve e a outra um Fa, mas não sabemos
qual é qual. X diz três frases
- X:
- Eu sou o Sinão.
- X:
- Y é um Fa.
- X:
- Z é um Ve.
- (b)
- O Sinão tem três irmãos--i1, i2, i3. Em cada sequência de
frases cada uma destas crianças mente exactamente uma vez, mas não
sabemos de antemão quando estão a mentir. Um dia as bolachas não
estavam na caixa habitual...Os testemunhos foram os seguintes.
- i1:
-
- i1 e i2 roubaram bolachas.
- O Sinão também roubou bolachas, mas eu não.
- i2:
-
- Eu não roubei nenhuma bolacha, mas o Sinão roubou.
- i1 roubou algumas bolachas.
- i3:
-
- i2 roubou algumas bolachas mas o i3 não.
- Eu não roubei nenhuma bolacha.
- (c)
- Sobre um dia escolar do Sinão os seus irmãos disserem o seguinte.
- i1:
-
- Foi à aula de Matemática.
- Não foi à aula de História.
- Não foi à aula de Biologia.
- i2:
-
- Foi à aula de História.
- Foi à aula de Inglês.
- Não foi à aula de Matemática.
- i3:
-
- Foi à aula de Matemática.
- Foi à aula de História.
- Não foi à aula de Inglês.
- (d)
- Sobre um exame de Matemática disseram as criancinhas o
seguinte.
- i1:
-
- A minha nota é menor que a do i2.
- i2 teve 70.
- i3 teve 30 mais do que o i2.
- i2:
-
- Tirei 60.
- Tirei 20 menos do que o i3.
- Tirei 10 mais do que o i1.
- i3:
-
- A minha nota é maior do que a do i2.
- A minha nota é 30 mais do que a de i1.
- A nota do i2 é 70.
- (e)
- Os pais perguntaram: Quantos rebuçados tem cada um de
vocês?
- i1:
-
- O i2 tem sete.
- Eu tenho menos do que o i2.
- O i3 tem três mais do que o i2.
- i2:
-
- Eu tenho seis.
- Tenho menos dois do que o i3.
- Tenho mais um do que o i1.
- i3:
-
- Não sou o que tem menos.
- Tenho mais três do que o i1.
- O i1 tem nove.
Quantos rebuçados tem cada criança, assumindo que cada uma mente exactamente uma vez?