- i)
- (a)
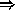 (b),
(b), - ii)
- (b)
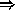 (a),
(a), - iii)
- (a)
 (b),
(b), - iv)
- nenhuma das anteriores.
- (a)
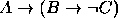 ,(b)
,(b) 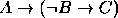 .
. - (a)
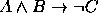 , (b)
, (b) 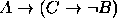 .
. - (a)
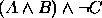 , (b)
, (b) 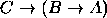
- (a)
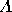 , (b)
, (b) 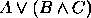 .
. - (a)
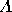 , (b)
, (b) 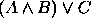 .
. - (a)
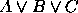 , (b)
, (b) 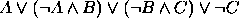 .
. - (a)
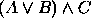 , (b)
, (b) 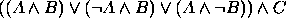 .
. - (a)
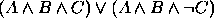 , (b)
, (b) 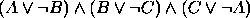 .
. - (a)
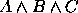 , (b)
, (b) 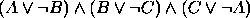 .
. - (a)
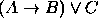 , (b)
, (b) 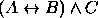
- (a)
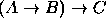 , (b)
, (b) 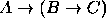 .
. - (a)
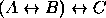 , (b)
, (b) 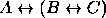 .
.
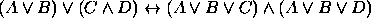 .
.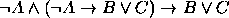 .
.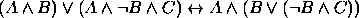 .
.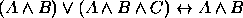 .
.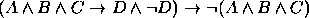 .
.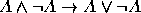 .
.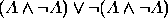 .
.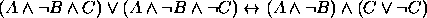 .
.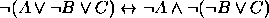 .
.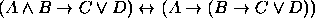 .
.
- Se o Óscar está na aula então a Maria ou a Virgínia também. A Maria não está na aula. Logo a Virgínia está na aula se o Óscar está na aula. (O, M, V).
- Se o Óscar está na aula a Maria também, e se a Maria está na aula o Gato também está. O Óscar está na aula a menos que o Gato esteja na aula. Logo a Maria não vai à aula. (O, M, G).
- Se o Óscar vai à aula então a Virgínia vai à aula só se o Gato vai à aula. O Gato vai à aula. Logo se o Óscar vai à aula a Virgínia também. (O, V, G).
- Se o Óscar e o Gato vão ambos à aula a Virgínia também vai. O Gato vai à aula. Logo ou a Virgínia vai à aula ou o Óscar não vai à aula. (O, G, V).
- Se O Óscar e o Gato vão à aula então ou a Maria ou a Virgínia vai à aula. Não é verdade que ou o Óscar ou a Maria vai à aula. Logo ou o Óscar ou a Virgínia vai à aula. (O, G, M, V).
- Se o Óscar e o Gato vão à aula então a Maria e a Virgínia também vão. Não é verdade que o Gato vá à aula só se a Virgínia for à aula. Logo o Óscar não vai à aula. (O, G, M, V).
- Uma condição necessária e suficiente para o Óscar ir à aula é que a Maria ou a Virgínia vá à aula. Uma condição suficiente para a Virgínia ir à aula é que o Gato vá. Contudo, o Gato não vai à aula a não ser que a Maria vá, e a Virgínia vai só se o Óscar for. Logo a Virgínia vai à aula se e só se o Óscar for. (O, M, V, G).
- Se o Óscar for à aula então nem a Maria nem a Virgínia vão. Se a Virgínia não for à aula então o Gato também não vai, mas se a Maria não for então o Gato vai. Logo o Óscar não vai à aula. (O, M, V, G).
- Premissas:
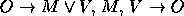
Conclusão:
 .
. - Premissas:
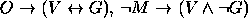
Conclusão:
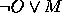 .
. - Premissas:
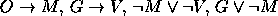
Conclusão:
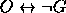 .
. - Premissas:
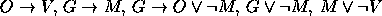
Conclusão:
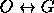 .
. - Premissas:
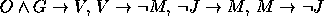
Conclusão:
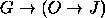 .
.Conclusão:
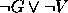 .
. - Premissas:
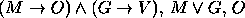
Conclusão:
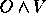 .
. - Premissas:
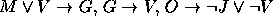
Conclusão:
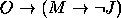 .
.
- Se
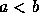 e
e 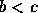 então
então
 . É verdade que
. É verdade que 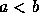 , mas não
se tem
, mas não
se tem  . Logo
. Logo 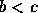 é falso.
é falso. - Se
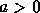 então uma condição necessária
e suficiente para
então uma condição necessária
e suficiente para 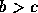 é que
é que 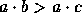 . É
verdade que se tem
. É
verdade que se tem 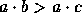 . Logo
. Logo 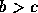 .
. - Se
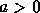 e
e 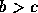 então
então
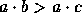 , e se
, e se 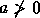 mas
mas 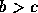 , então
, então 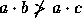 . Logo
. Logo 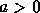 se e só se
se e só se 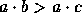 .
. - Se
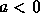 e
e 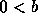 , então
, então
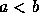 . Se
. Se 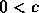 e
e 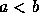 ,
então
,
então 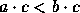 . Acontece que
. Acontece que 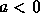 e
e 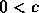 . Logo
. Logo 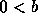 só se
só se 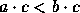 .
. - Uma condição necessária e suficiente para
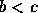 é que
é que 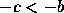 . Além disso, se
. Além disso, se 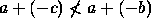 , então
, então 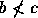 . Logo
. Logo 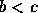 sse
sse 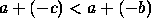 .
. - Se
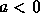 e
e 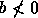 então
então
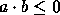 . Se
. Se 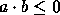 , então se
, então se 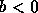 tem-se
tem-se 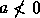 . Se
. Se 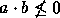 então ou se tem
então ou se tem 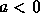 e
e 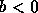 , ou
, ou 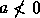 e
e 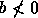 . Se
. Se
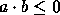 e
e 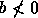 então
então 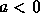 .
Logo, uma condição necessária e suficiente para
.
Logo, uma condição necessária e suficiente para 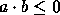 é que
é que 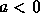 sse
sse 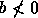 .
. 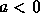 ou
ou 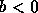 .
Tem-se também que
.
Tem-se também que 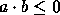 se
se 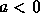 e
e
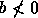 ou se
ou se 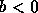 e
e 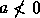 .
Logo, se não se tiver simultaneamente
.
Logo, se não se tiver simultaneamente 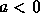 e
e
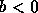 então
então 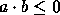 .
.-
- Defina-se uma função
 por
por
Logo
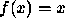 ou
ou 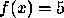 .
.[Sugestão: Seja Z:
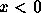 ; X:
; X: 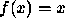 ; F:
; F: 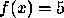 ].
]. - Defina-se uma função
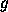 por
por
onde
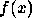 foi definida na alínea
anterior. Assuma que
foi definida na alínea
anterior. Assuma que 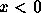 ou
ou 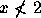 . Logo
. Logo 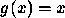 ou
ou 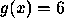 .
.[Sugestão: Se Z:
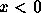 e T:
e T: 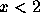 ,
então
,
então 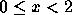 é
é 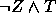 . Seja X:
. Seja X:
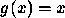 ; F:
; F: 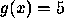 ; S:
; S: 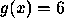 ].
]. - Seja
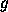 a função definida acima.
Assuma que nem
a função definida acima.
Assuma que nem 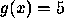 nem
nem 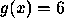 .
Logo
.
Logo 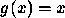 .
.
- Defina-se uma função
- Se
 é contínua em
é contínua em 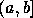 , então
, então  tem um máximo em
tem um máximo em
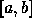 se estiver definida em
se estiver definida em  . Se
. Se
 não estiver definida em
não estiver definida em  , então
existe um ponto
, então
existe um ponto  entre
entre  e
e
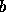 tal que
tal que 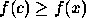 para todo o
para todo o
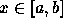 . Se existe um tal ponto
. Se existe um tal ponto  entre
entre
 e
e 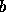 tal que
tal que 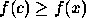 para todo o
para todo o 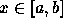 , então
, então
 tem um máximo em
tem um máximo em 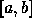 .
.
- Logo
 tem um máximo em
tem um máximo em 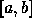 .
. - Logo, se
 é contínua em
é contínua em 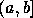 , então
, então  tem um máximo em
tem um máximo em
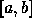 .
.
- Logo
- Uma condição necessária para
 ter um máximo em
ter um máximo em
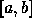 é que
é que  seja contínua em
seja contínua em
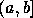 e
e  esteja definida em
esteja definida em
 . Uma condição necessária e suficiente para
. Uma condição necessária e suficiente para
 ter um máximo em
ter um máximo em 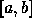 é que
exista um ponto
é que
exista um ponto  entre
entre  e
e
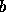 tal que
tal que 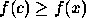 para todo o
para todo o
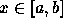 . De facto, existe um ponto
. De facto, existe um ponto  entre
entre
 e
e 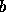 tal que
tal que 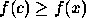 para todo o
para todo o 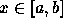 . Logo
. Logo  é contínua em
é contínua em 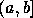 e
e  está definida em
está definida em  . [Use as letras
do problema 9].
. [Use as letras
do problema 9]. - Se
 é substituído por um e dois
na desigualdade
é substituído por um e dois
na desigualdade 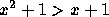 , obtemos
, obtemos 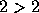 e
e 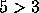 , respectivamente. Contudo
, respectivamente. Contudo
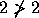 , mas
, mas 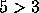 . Logo não substituímos
. Logo não substituímos
 por um na desigualdade
por um na desigualdade 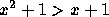 , mas
sim por dois. [Use as letras A, B, C:
, mas
sim por dois. [Use as letras A, B, C: 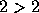 , e D:
, e D:
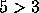 para as proposições atómicas].
para as proposições atómicas]. - Se
 é substituído por um e dois
na desigualdade
é substituído por um e dois
na desigualdade 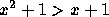 , obtemos
, obtemos 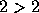 e
e 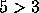 , respectivamente. Contudo
não se tem
, respectivamente. Contudo
não se tem 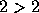 mas
mas 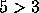 .
Logo não substituímos
.
Logo não substituímos  por um e por dois na
desigualdade
por um e por dois na
desigualdade 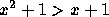 . [Use as letras do problema
11].
. [Use as letras do problema
11].
- Premissas:
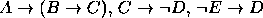
Conclusão:
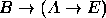 .
. - Premissas:
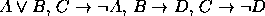
Conclusão:
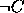 .
. - Premissas:
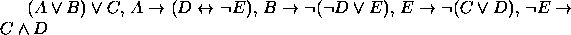
Conclusão:
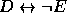 .
. - Premissas:
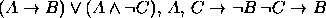
Conclusão:
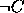 .
. - Premissas:
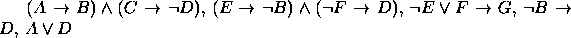
Conclusão:
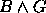 .
. - Premissas:
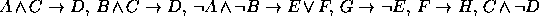
Conclusão:
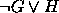 .
. - Premissas:
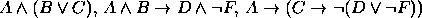
Conclusão:
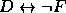 .
. - Premissas:
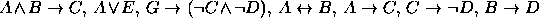
Conclusão:
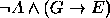 .
. - Premissas:
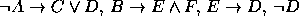
Conclusão:
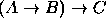 .
. - Premissas:
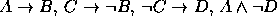
Conclusão:
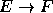 .
. - Premissas:
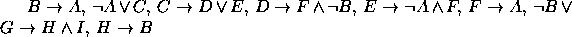
Conclusão:
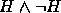 .
. - Premissas:
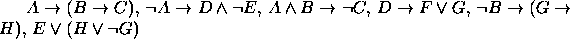
Conclusão:
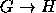 .
.