Problemas

1. Traduza cada uma das frases para a linguagem do cálculo proposicional. [Atribua letras às proposições atómicas e use conectivos e parenteses.]
   1. O Óscar e a Virgínia vão à escola.
   2. O Óscar inscreveu-se em Lógica, mas a Virgínia não.
   3. Nem o Óscar nem a Virgínia gostam do Pôncio.
   4. Se o Óscar sai com a Virgínia então o Pôncio não.
   5. O Óscar sai com a Virgínia ou o Pôncio sai com a Virgínia, mas não ambos.
   6. O Óscar passa a Lógica só se estudar.
   7. O Óscar não passa a Lógica a não ser que faça o trabalho de casa e estude.
   8. O Óscar não passa a Lógica se não fizer o trabalho de casa nem estudar.
   9. Não é verdade que Óscar passe a Lógica desde que faça o trabalho de casa e estude.
   10. Uma condição suficiente para Óscar passar a Lógica é que ele estude e faça o trabalho de casa.
   11. Se o Óscar não estudar e fizer o trabalho de casa então ele não passa a Lógica.
   12. Se o Óscar e a Virgínia trabalharem a um ritmo constante então não há perda nem ganho de eficiência quando trabalham juntos.
   13. Se perder o meu combóio chego 10 minutos atrazado, assumindo que o próximo vem à tabela.
   14. Vamos hoje ao parque desde que o carro não se estrague e não chova.
   15. Se Lógica é difícil o Óscar e a Virgínia só passam se estudarem.
   16. Se duas rectas são complanares uma condição necessária e suficiente para serem paralelas é que não se intersectem nem coincidam.
   17. Se Q é um quadrilátero então Q é um paralelogramo sse os seus lados opostos são paralelos e iguais.
   18. Se a função f é contínua no intervalo (a,b) então f tem um máximo em [a,b] ou f não é contínua em a e b.
   19. Uma condição suficiente para a função f ter um máximo em [a,b] é que f seja contínua em (a,b) e que f seja contínua em ambos a e b.
   20. Se f' está definida num intervalo (a,b), uma condição necessária e suficiente para f ser crescente em (a,b) é que f' seja positiva em (a,b).
   21. Uma condição necessária e suficiente para f' ser positiva em (a,b) é que f' esteja definida em (a,b) e f seja crescente em (a,b).
   22. Se e A é uma aproximação de I obtida pelo método do trapézio então se f'' >0 para .
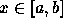   23. Se 3 e 4 forem substituir x e y, respectivamente, na desigualdade 2x+y<x+3y obtemos a desigualdade 10<15.
   24. Se 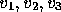são três vectores de 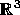aplicados na origem, então o conjunto 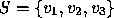é linearmente independente sse os três vectores estão no mesmo plano.
2. Atribua letras às proposições atómicas e traduza cada uma das seguintes frases numa fórmula lógica.
   1. Se a Virgínia passou a Lógica ou a Geometria então ela foi aceite na universidade.
   2. Se a Virgínia não passar a Lógica e a Geometria então não será aceite em Harvard nem Yale.
   3. Não é verdade que se o Óscar arranjar emprego se case com a Virgínia.
   4. Óscar procurará emprego se chumbar, a não ser que vá para uma escola técnica.
   5. O Óscar e a Virgínia acabam a licenciatura só se passarem a Lógica.
   6. Uma condição necessária e suficiente para que três pontos A,B,C estejam na mesma recta é que a distância de A a C seja a soma da distância de A a B com a distância de B a C.
   7. Se f é contínua e diferenciável em [a,b], então há uma tangente horizontal ao gráfico de f entre a e b ou f(a) e f(b) não se anulam simultaneamente.
   8. Uma condição necessária para f ser contínua em x=a é que f(a) esteja definido e exista.
   9. Se x é um número inteiro então exactamente um número de entre x e x+1 é par.
   10. Se f é contínua mas não integrável em (a,b) então f não está definida simultanemante em a e b.
   11. Se A é uma proposição falsa então a proposição condicional 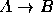tem a forma 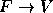ou 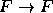, conforme B é verdadeira ou falsa, respectivamente.
   12. Se f é uma função e f tem derivadas contínuas numa vizinhança de 0, V, para 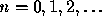então

       sse o resto,

       converge para zero quando n cresce sem limite.

3. Determine a recíproca, inversa e contra-recíproca de cada uma das seguintes proposições condicionais.
   1. Se v é paralelo a w então .
   2. Duas rectas intersectam-se se não são paralelas.
   3. Se o Óscar se licenciar ele vai procurar emprego ou inscrever-se num curso de mestrado.
   4. Se a Virgínia se licenciar e se inscrever num curso de mestrado então a sua licenciatura não é de Matemática.
   5. Se a Virgínia se licenciar com boa média a Matemática ela vai ter uma bolsa para se inscrever num curso de mestrado.
   6. Passar a Álgebra é uma condição necessária para o Belo se licenciar.
   7. Uma condição suficiente para um triângulo satisfazer o Teorema de Pitágoras é ser um triângulo rectângulo.
   8. Uma condição necessária para dois triângulos serem semelhantes é que tenham lados iguais.
   9. Um triângulo é equilátero só se os seus três ângulos são iguais ou os seus três lados são iguais.
   10. Três pontos estão sobre a mesma circunferência só se não forem colineares.
4. Determine a tabela de verdade de cada uma das fórmulas seguintes.
   1. 
   2. 
   3. 
   4. 
   5. 
5. Mostre que cada um dos seguintes pares de fórmulas partilham a mesma tabela de verdade.
   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 
   8. 
6. Construa uma árvore a partir de letras proposicionais para cada uma das seguintes fórmulas.
   1. 
   2. 
   3. 
   4. 
   5.