


Next: Problemas Up: Estruturas Interpretativas
Previous: Estruturas Interpretativas
Seja  uma fórmula com, no máximo, n
variáveis livres:
uma fórmula com, no máximo, n
variáveis livres: 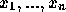 . Seja S uma estrutura
interpretativa para
. Seja S uma estrutura
interpretativa para  . Seja
. Seja 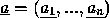 um n-uplo de elementos de
um n-uplo de elementos de 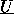 , onde
, onde
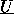 é o universo de S.
é o universo de S.
- I.
- Seja t um termo em
 .
.
- Caso 1.
- t é
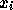 ou
ou 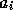 .
Então
.
Então 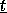 é
é 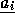 .
.
- Caso 2.
- t é
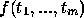 . Então
. Então 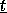 é
é 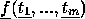 .
.
- II.
- Seja
 uma fórmula atómica. Neste
caso
uma fórmula atómica. Neste
caso  tem a forma
tem a forma 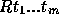 onde
onde 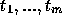 são termos. Seja
são termos. Seja 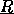 a interpretação de R em S e
a interpretação de R em S e 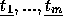 as
interpretações de
as
interpretações de 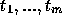 , respectivamente. O n-uplo
, respectivamente. O n-uplo
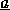 satisfaz
satisfaz  em S sse
em S sse
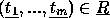 .
.
[No caso de  não conter variáveis livres a
interpretação de
não conter variáveis livres a
interpretação de  em S independe de
em S independe de 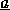 , portanto todos os n-uplos satisfazem a fórmula, ou
nenhum o faz].
, portanto todos os n-uplos satisfazem a fórmula, ou
nenhum o faz].
- III.
- Seja
 obtida das fórmulas
obtida das fórmulas
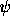 e
e 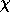 usando conectivos. Temos os
seguintes casos:
usando conectivos. Temos os
seguintes casos:
- Caso 1.
 é
é 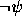 .
.
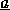 satisfaz
satisfaz  em S sse
em S sse 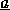 não satisfaz
não satisfaz 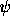 em S.
em S.
- Caso 2.
 é
é 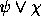 .
.
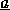 satisfaz
satisfaz  em S sse
em S sse 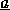 satisfaz
satisfaz 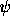 em S ou
em S ou 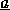 satisfaz
satisfaz 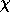 em S.
em S.
- Caso 3.
 é
é 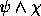 .
.
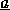 satisfaz
satisfaz  em S sse
em S sse 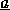 satisfaz
satisfaz 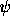 em S e
em S e 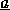 satisfaz
satisfaz 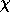 em S.
em S.
- Caso 4.
 é
é 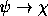 .
.
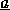 satisfaz
satisfaz  em S sse
em S sse 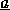 não satisfaz
não satisfaz  em S ou
em S ou 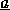 satisfaz
satisfaz  em S.
em S.
- Caso 5.
 é
é 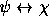 .
.
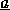 satisfaz
satisfaz  em S sse
em S sse 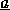 satisfaz
satisfaz  e
e 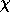 em S ou
em S ou 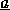 não satisfaz
não satisfaz  nem
nem 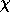 em S.
em S.
- IV
 é
é 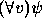 ou
ou
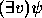 . Seja
. Seja 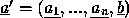 . [A fórmula
. [A fórmula
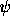 pode ter
pode ter  como variável livre;
como variável livre;
 é substituído por
é substituído por 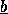 nas
interpretações abaixo].
nas
interpretações abaixo].
- Caso 1.
 é
é 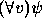 .
.
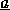 satisfaz
satisfaz  em S sse
em S sse 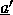 satisfaz
satisfaz 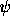 em S para qualquer
em S para qualquer 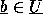 .
.
- Caso 2.
 é
é 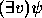 .
.
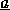 satisfaz
satisfaz  em S sse
em S sse 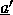 satisfaz
satisfaz 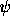 em S para algum
em S para algum 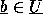 .
.
Seja  uma fórmula com, no máximo, n
variáveis livres, S uma estrutura interpretativa para
uma fórmula com, no máximo, n
variáveis livres, S uma estrutura interpretativa para  ,
, 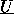 o universo de S.
o universo de S.
- 1.
 é verdadeira em S sse
qualquer n-uplo de elementos de
é verdadeira em S sse
qualquer n-uplo de elementos de 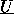 satisfaz
satisfaz
 .
.- 2.
 é falsa em S sse
nenhum n-uplo de elementos de
é falsa em S sse
nenhum n-uplo de elementos de 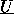 satifaz
satifaz
 .
.
[Há fórmulas que não são verdadeiras nem falsas numa estrutura
interpretativa, mas nenhuma fórmula pode ser verdadeira e falsa].
Uma fórmula  é válida (ou
universalmente válida) se
é válida (ou
universalmente válida) se  é verdadeira em
todas as estruturas interpretativas para
é verdadeira em
todas as estruturas interpretativas para  .
.



Next: Problemas Up: Estruturas Interpretativas
Previous: Estruturas Interpretativas
Jorge Nuno Silva (Dep. Mat. FCUL)
Wed Jun 4 19:06:16 MET DST 1997
![]() uma fórmula com, no máximo, n
variáveis livres:
uma fórmula com, no máximo, n
variáveis livres: ![]() . Seja S uma estrutura
interpretativa para
. Seja S uma estrutura
interpretativa para ![]() . Seja
. Seja ![]() um n-uplo de elementos de
um n-uplo de elementos de ![]() , onde
, onde
![]() é o universo de S.
é o universo de S.![]() não conter variáveis livres a
interpretação de
não conter variáveis livres a
interpretação de ![]() em S independe de
em S independe de ![]() , portanto todos os n-uplos satisfazem a fórmula, ou
nenhum o faz].
, portanto todos os n-uplos satisfazem a fórmula, ou
nenhum o faz].![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() não satisfaz
não satisfaz ![]() em S.
em S.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() satisfaz
satisfaz ![]() em S ou
em S ou ![]() satisfaz
satisfaz ![]() em S.
em S.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() satisfaz
satisfaz ![]() em S e
em S e ![]() satisfaz
satisfaz ![]() em S.
em S.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() não satisfaz
não satisfaz ![]() em S ou
em S ou ![]() satisfaz
satisfaz ![]() em S.
em S.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() satisfaz
satisfaz ![]() e
e ![]() em S ou
em S ou ![]() não satisfaz
não satisfaz ![]() nem
nem ![]() em S.
em S.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() satisfaz
satisfaz ![]() em S para qualquer
em S para qualquer ![]() .
.![]() satisfaz
satisfaz ![]() em S sse
em S sse ![]() satisfaz
satisfaz ![]() em S para algum
em S para algum ![]() .
.![]() é válida (ou
universalmente válida) se
é válida (ou
universalmente válida) se ![]() é verdadeira em
todas as estruturas interpretativas para
é verdadeira em
todas as estruturas interpretativas para ![]() .
.