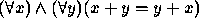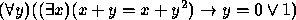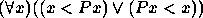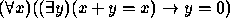Problemas

A.

Traduza cada uma das seguintes frases para a linguagem do Cálculo de Predicados. Use as letras propostas para as constantes, símbolos de função e símbolos de predicado.

1. Todos os pássaros são animais. (Px, Ax)
2. Alguns gatos não têm cauda. (Gx, Cx)
3. Nem todas as plantas precisam de sol. (Px, Sx)
4. Nenhum aluno desta turma gosta de Física. (Ax, Tx, Fx)
5. Alguns estudantes gostam de Física e alguns gostam de Matemática. (Ex, Fx, Mx)
6. Alguns estudantes que gostam de Física também gostam de Matemática. (Ex, Fx, Mx)
7. O Óscar e a Maria são estudantes que gostam de Matemática. (o, m, Ex, Mx)
8. O aluno mais baixo desta turma gosta de Matemática mas não gosta de Física. (b, Mx, Fx)
9. Só estudantes que gostam de Física gostam de Matemática. (Ex, Fx, Mx)
10. De entre os estudantes do curso de Matemática só os que fizerem o trabalho de casa terão nota alta. (Ex, Mx, Tx, Ax)
11. O Óscar e o Jorge gostam da Maria. (o, j, m, Gxy)
12. Se a Maria é mais velha que a Virgínia e a Virgínia é mais velha que a Teresa, então a Maria é mais velha que a Teresa. (m, v, t, Vxy)
13. Todo o estudante que for mais velho que a Maria também é mais velho que a Virgínia. (m, v, Ex, Vxy)
14. Todos os professores são mais velhos que todos os estudantes. (Px, Ex, Vxy)
15. Todo o professor que for mais velho que o Óscar também é mais velho que algum estudante. (o, Px, Ex, Vxy)
16. Nem todos os professores que são mais velhos que o Óscar são mais velhos que todos os estudantes. (o, Px, Ex, Vxy)
17. Ninguém é mais velho que ele mesmo. (Vxy)
18. Se alguém é mais velho que o Óscar então todos os estudantes são mais velhos que o Óscar. (o, Ex, Vxy)
19. Qualquer estudante que goste de todos os professores também gosta de si mesmo. (Ex, Px, Gxy)

    Nos exercícios 20--26 use os seguintes símbolos de predicados e constantes:

    Fx: x é professor

    Ex: x é estudante

    Mx: x vai a um meeting

    Axy: x está acompanhado de y

    Pxy: x é progenitor de y

    j: Jorge

    m: Maria

20. Todos os estudantes e professores assistem ao meeting.
21. Nenhum estudante que assiste ao meeting é acompanhado de um professor.
22. Algum progenitor de um estudante não assistiu ao meeting.
23. Se todos os professores assistem ao meeting então algum estudante é acompanhado por um professor.
24. O Jorge e a Maria assistiram ao meeting mas nenhum deles foi acompanhado por um estudante.
25. Nenhum professor acompanhado pelo Jorge assistiu ao meeting.
26. Se nem o Jorge nem a Maria são acompanhados por um estudante, então nenhum estudante assiste ao meeting.

    Nos exercícios 27--38 use os seguintes símbolos de predicados e constantes:

    Ex: x é um estudante-piloto

    Ix: x é instrutor

    Cx: x é uma cidade

    Vxyz: x pilota um avião para y acompanhado de z

    c: Costa da Caparica

27. Algum estudante-piloto pilota um avião para a Costa da Caparica acompanhado por um instrutor.
28. Algum estudante-piloto pilota um avião para alguma cidade acompanhado por um instrutor.
29. Todos os instrutores têm um aluno que pilota, com eles, um avião para alguma cidade.
30. Quem pilota aviões para quaisquer cidades acompanhados de instrutores são os estudantes-pilotos.
31. Nem todos os instrutores que pilotam aviões para alguma cidade acompanhados de um instrutor são estudantes-pilotos.
32. Estudantes-pilotos que pilotam um avião para a Costa da Caparica acompanhados de um estudante-piloto são instrutores.
33. Somente um instrutor pode pilotar um avião para a Costa da Caparica acompanhado de um estudante-piloto.
34. Há um instrutor tal que todos os estudantes-pilotos voam para a Costa da Caparica com ele.
35. Nenhum instrutor voa para todas as cidades com um estudante-piloto.
36. Algum estudante-piloto que voa para todas as cidades sem companhia é um instrutor.
37. Nenhum estudante-piloto que não pilota um avião para todas as cidades com um instrutor é um instrutor.
38. Qualquer estudante-piloto que não pilota um avião para todas as cidades sem companhia não é instrutor.

    Nos exercícios 39--50 use os seguintes símbolos de predicados e constantes:

    Dx: x é um estudante

    Ex: x é um exame

    Pxy: x é um problema no exame y

    Rxy: x resolve y

    f(x,y): o x-ésimo problema no exame y

    g(x): o problema mais fácil do exame x

    h(x): o problema mais difícil do exame x

    a: Alexandre

    n: Natacha

    1: um

    2: dois

    3: três

39. Nenhum estudante resolve o problema um do exame três.
40. Natacha resolve o problema mais difícil do exame um, mas não resolve o problema mais fácil do exame dois.
41. Se todos os estudantes resolverem o problema mais difícil do exame dois então o Alexandre e a Natacha também.
42. Todos os estudantes que resolvem o problema um do exame um também resolvem o problema mais fácil do exame um.
43. Se algum estudante resolve todos os problemas de todos os exames então algum estudante resolve o problema mais difícil de cada exame.
44. Algum estudante que resolve todos os problemas do exame um não resolve o problema um do exame dois.
45. Cada estudante resolve algum problema em cada exame.
46. Só estudantes resolvem todos os problemas de algum exame.
47. Nenhum aluno resolve todos os problemas dum exame.
48. Os estudantes que resolvem todos os problemas dum exame também resolvem todos os problemas de todos os exames.
49. Quem resolve um problema dum exame é um estudante.
50. Se algum estudante resolve algum problema de cada exame então algum estudante resolve o problema mais fácil de todos os exames.

B.

Traduza cada uma das seguintes frases para a linguagem do Cálculo de Predicados. Utilize constantes, símbolos de predicado e de função da lista abaixo.

Assuma que as variáveis tomam valores no conjunto dos números inteiros.

Use as expressões matemáticas comuns, por exemplo: "x é múltiplo de y" é sinónimo de "y é um factor de x" e de "existe z tal que x=y z.

: x é maior que y

: x é maior ou igual a y

: x é igual a y

[Pode usar em vez de , etc.]

x+y: a soma de x e y

x y: o produto de x e y

Pode também usar-se "-1", "-2", "0", "1", "2", etc. com o significado usual.

1. A propriedade comutativa da adição.
2. A propriedade distributiva da multiplicação relativamente à adição.
3. Alguns inteiros são múltiplos de três.
4. Nem todos os inteiros são múltiplos de cinco.
5. Dez é um múltiplo positivo de algum número.
6. Todos os múltiplos positivos de sete são maiores que cinco.
7. Nenhum múltiplo positivo de cinco é menor que sete.
8. Dois é o menor par positivo.
9. Existe o menor ímpar positivo.
10. Existe pelo menos um inteiro entre cinco e dois. [Pode assumir que se sabe que dois é menor que cinco].
11. Todos os inteiros têm inverso aditivo.
12. Nem todos os inteiros não nulos têm inverso multiplicativo.
13. A soma de dois ímpares é par.
14. O produto de um inteiro por um par é um par.
15. Algum ímpar é factor de todos os pares.
16. Cada par é múltiplo de algum ímpar.
17. Há dois inteiros que têm a mesma paridade e são ambos múliplos de sete.
18. Não é verdade que se dois números têm a mesma paridade então são ambos múltiplos de três.
19. Se dois números diferentes têm a mesma paridade então os seus quadrados também.
20. Qualquer par de inteiros distintos com a mesma paridade tem um inteiro entre eles.

    Nos exercícios 21--24 assuma que uma equação linear tem a forma

21. Algumas equações lineares têm soluções inteiras.
22. Uma equação linear tem soluções inteiras sse o coeficiente director é um divisor do termo constante.
23. Nenhuma equação linear tem duas soluções distintas.
24. Para qualquer equação linear, se os coeficientes são ambos ímpares então a solução também é ímpar, a menos que não haja solução inteira.

C.

Traduza cada uma das seguintes fórmulas do Cálculo de Predicados para Português. Use o dicionário seguinte:

Cx: x é um gato

Dx: x é um cão

Tx: x tem cauda

Bxy: x morde y

Lxy: x gosta de y

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 

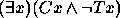
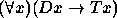
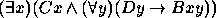
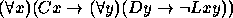
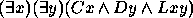
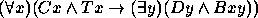
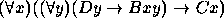
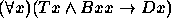
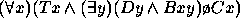
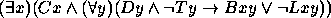
    Para os exercícios 11--20 use o seguinte dicionário:

    a: Alexandre

    n: Natacha

    Pxy: x é um problema no exame y

    Ex: x é um exame

    Mx: x é um homem

    Wx: x é uma mulher

    Sxy: x resolve y

11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 

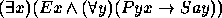
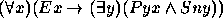
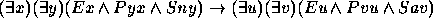
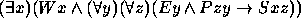
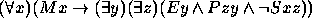
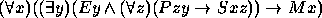
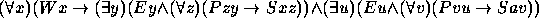
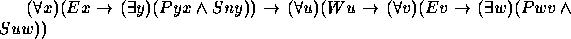
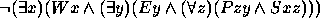
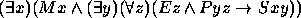
    Nos exercícios 21--30 use o seguinte dicionário:

    Ix: x é um inteiro

    x y: x é menor que y

    x y: x é menor ou igual a y

    x=y: x é igual a y

    x+y: a soma de x e y

    x-y: a diferença de x e y

    x y: o produto de x e y

    Use os símbolos usuais para números reais e assuma que as variáveis tomam valores no conjunto dos números reais. "x 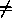y" é uma abreviatura de " (x=y)".

21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 

D.

Traduza cada uma das seguintes frases para a linguagem do Cálculo de Predicados.

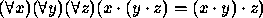
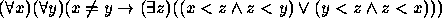
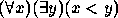
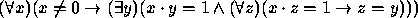
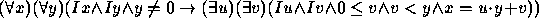
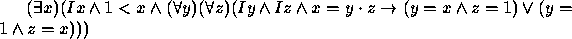
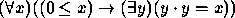
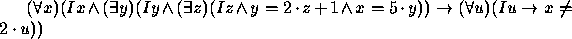
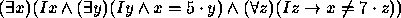
1. Todos os professores que fazem investigação gostam de ensinar. O Silveira é um professor que não gosta de ensinar. Há professores que não fazem investigação.
2. Zelda e Zanzibar são dois gatos que moram num celeiro. Zelda caça todos os ratos, mas Zanzibar não caça nenhum. Todos os ratos têm medo da Zelda, mas há ratos que não têm medo do Zanzibar. Nenhum rato vive no celeiro.
3. Cada problema é resolvido por algum aluno. O Óscar resolve alguns problemas. Algum estudante resolve todos os problemas. Nenhum estudante não resolve nenhum problema.
4. Todo o estudante estuda algum assunto com algum professor. Nenhum estudante estuda todos os assuntos com todos os professores. Há um assunto que todos os estudantes estudam com algum professor. Todo o estudante que estuda todos os assuntos sem outra companhia é um professor.
5. Alguém é atropelado todos os dias. O Óscar é atropelado na segunda-feira. O Óscar e a Capitulina são atropelados na terça-feira, mas ninguém é atropelado na sexta-feira.
6. Alguns inteiros são pares, alguns são ímpares. Nenhum inteiro é par e ímpar. Se um inteiro é par o seu sucessor é ímpar; se um inteiro é ímpar o seu sucessor é par.
7. Todo o inteiro é múltiplo de algum inteiro. Há um inteiro que só é múltiplo de si mesmo. Todo o inteiro é múltiplo de si mesmo.
8. Todo o inteiro tem pelo menos um inverso aditivo. Dois inteiros diferentes não têm o mesmo inverso aditivo. Se um inteiro tem x como inverso aditivo e outro tem -x como inverso aditivo, então a sua soma é zero, para qualquer x.

E.

Identifique as ocorrências livres da variável x nas seguintes fórmulas:

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 

F.

Classifique cada uma das seguintes expressões como:

i)

termos,

ii)

fórmulas atómicas,

iii)

fórmulas não atómicas,

iv)

sentenças,

v)

nenhum dos anteriores.

1. Cada estudante desta turma vai passar.
2. O aluno mais alto desta turma.
3. O Óscar é mais alto do que o aluno sentado na primeira cadeira da primeira fila.
4. Mariana ou Pedro.
5. O aluno com melhores notas da escola x.
6. x está entre 2 e y.
7. Flores.
8. Flores amarelas.
9. Amarelo.
10. Flores implica Inverno frio.
11. A flor mais bonit do jardim do x é amarela.
12. As flores do jardim do Pedro são amarelas ou vermelhas.
13. A Natércia escreve à máquina com rapidez e precisão.
14. Escreve à máquina com rapidez.
15. Com precisão.
16. .
17. 
18. 
19. .
20. .
21. .
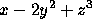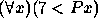
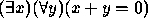
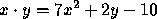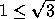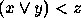22. Px=Qxy.
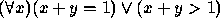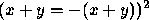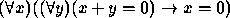23. .
24. .
25. .
26. .
27. 
28. 
29. 
30. 

G.

Construa uma árvore a partir de fórmulas atómicas para cada uma das seguintes fórmulas.

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10.