|
Definições
|
|
I. Ponto é o, que
não tem partes, ou o, que não tem grandeza alguma.
|
|
II. Linha é o, que
tem comprimento sem largura.
|
|
III. As
extremidades da linha são pontos.
|
|
IV. Linha recta é
aquella, que está posta egualmente entre as suas
extremidades.
|
|
V. Superfície é o,
que tem comprimento e largura.
|
|
VI. As extremidades
da superfície são linhas.
|
|
VII. Superfície
plana é aquella, sobre a qual assenta toda uma linha recta entre
dous pontos quaesquer, que estiverem na mesma
superfície.
|
|
VIII. Angulo plano
é a inclinação reciproca de duas linhas, que se tocam em uma
superfície plana, sem estarem em direitura uma com a
outra.
|
|
IX. Angulo plano
rectilineo é a inclinação reciproca de duas linhas rectas, que se
encontram, e não estão em direitura uma com outra.
|
|
Se alguns angulos existirem no mesmo
ponto B, cada um delles vem indicado com tres letras do alfabeto; e
a, que estiver no vertice do angulo, isto he, no ponto, no qual se
encontram as rectas, que formam o angulo, se põe no meio das outras
duas; e destas uma está posta perto de uma das ditas rectas, em
alguma parte, e a outra perto da outra linha. Assim o angulo feito
pelas rectas AB, CB representar-se-ha com as letras ABC, ou CBA; o
angulo formado pelas rectas AB, DB, com as letras ABD, ou DBA; e o
angulo que fazem as rectas DB, CB, com as letras DBC, ou CBD. Mas,
se um angulo estiver separado de outro qualquer, poder-se-ha marcar
com a mesma letra, que estiver no vertice, como o angulo no ponto
E.
|
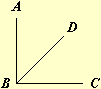 |
|
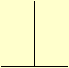
X. Quando uma linha
recta, caindo sobre outra linha recta, fizer com esta dous angulos
eguaes, um de uma, e outro de outra parte, cada um destes angulos
eguaes se chama angulo recto; e a linha incidente se diz
perpendicular á outra linha, sobre a qual cae.
|
 |
|
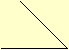
XI. Angulo obtuso é
o, que é maior, que o angulo recto.
|
|
XII. Angulo agudo é
o, que é menor, que o angulo recto.
|
 |
|
XIII. Termo se diz
aquillo, que é extremidade de alguma cousa.
|
|
XIV. Figura é um
espaço, fechado por um ou mais termos.
|
|
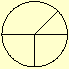
XV. Circulo é uma
figura plana, fechada por uma só linha, a qual se chama
circumferencia: de maneira que todos as linhas rectas, que de um
certo ponto existente no meio da figura, se conduzem para a
circumferencia, são eguaes entre si.
|
 |
|
XVI. O dicto ponto
se chama centro do circulo.
|
|
XVII. Diametro do
circulo é uma linha recta,que passa pelo centro, e que se termina
por ambas as partes na circumferencia.
|
|
XVIII. Semicirculo
é uma figura, comprehendida entre o diametro e aquella parte da
circumferencia do circulo, que é cortada pelo
diametro.
|
|
XIX. Segmento de
circulo é uma figura, comprehendida entre uma linha recta e uma
porção da circumferencia.
|
|
XX. Figuras
rectilineas são as, que são formadas com linhas
rectas.
|
|
XXI. As trilateras
são aquellas, que são formadas com tres linhas rectas.
|
|
XXII. As
quadrilateras são aquellas, que são feitas por quatro linhas
rectas.
|
|
XXIII. As
multilateras são as, que são feitas por mais de quatro linhas
rectas.
|
|
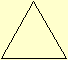
XXIV. Entre as
figuras trilateras o triangulo equilatero é o, que tem os tres
lados eguaes.
|
 |
|
XXV. Triangulo
isosceles é o, que tem dous lados eguaes.
|
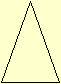 |
|
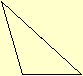
XXVI. Triangulo
scaleno é o, que tem os tres lados desiguaes.
|
 |
|
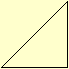
XXVII. Triangulo
rectangulo é o, que tem um angulo recto.
|
 |
|
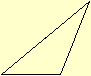
XXVIII. Triangulo
obtusangulo é o, que tem um angulo obtuso.
|
 |
|
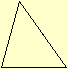
XXIX. O triangulo
acutangulo é o, que tem todos os angulos agudos.
|
 |
|
XXX. Entre as
figuras quadrilateras o quadrado é o, que é junctamente equilatero
e rectangulo.
|
 |
|
XXXI. E a figura,
que de uma parte for mais comprida, pode ser rectangula, mas não
equilatera.
|
|
XXXII. Mas o rhombo
é uma figura equilatera, e não rectangula.
|
 |
|
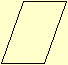
XXXIII. Rhomboide é
uma figura, que, tendo os lados opostos eguaes, nem é equilatera
nem equiangula.
|
 |
|
XXXIV. Todas as
mais figuras quadrilateras, que não são as referidas, se chamam
trapezios.
|
|
XXXV. Linhas
parallelas ou equidistantes são linhas rectas, que existindo no
mesmo plano, e sendo produzidas de ambas as partes, nunca se chegam
a tocar.
|